Coding Questions - Graph¶
Basics¶
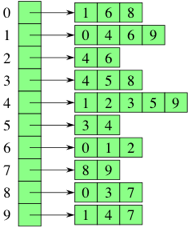
Graph Representation: Here’s a good `tutorial`__.
- How long it takes to determine whether a given edge is in the graph
- Adjacency lists
- Edge lists
- How long it takes to find the neighbors of a given vertex
- Adjacency matrices
The most used or nataural way is to use Adjacency lists:
Or we can use OOD concept to store vertex information.
Topological Sort: Topological Sorting for a graph is not possible if the graph is not a DAG.
An ordering of its vertices along a horizontal line so that all directed edges go from left to right.
- Doing with DFS:
- Doing with BFS:
LeetCode 207. Course Schedule¶
My thought is clear and i construct a graph using dictionary, then i can do a BFS on this graph until number of courses has met. However, i failed to detect the circle and handle that case. This is really a good chance for me to learn this kind of graph related questions.
Or saying from `website`__ this prerequisite relationship reminds one of directed graphs. Then, the problem reduces to find a topological sort order of the courses, which would be a DAG if it has a valid order.
This problem can be solved in 3 different ways: #. Detecting a cycle DFS.(Don’t use BFS) #. Using topological sort. (BFS/DFS) #. Union-Find?
If you treat it as a cycle detection problem, you can use a graph traversal method and detect a cycle along the traverse. Thus there’re 2 versions of cycle detection.
DFS:
# Adjacency List solution to detect cycle
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
from collections import defaultdict
graph = defaultdict(list)
# initilize the graph
# since the question is assuming we will have n courses in total which makes
# initializing the graph much easier.
def buildGraph(graph, numCourses, edgelists):
for i in range(numCourses):
graph[i]
for edge in edgelists:
graph[edge[1]].append(edge[0])
return graph
graph = buildGraph(graph, numCourses, prerequisites)
WHITE = 1
BLACK = 2
GREY = 3
self.visited = [WHITE for _ in range(numCourses)]
self.circle = 0
def DFS_Visit(graph, vertex):
self.visited[vertex] = GREY
for adj_vertex in graph[vertex]:
if self.visited[adj_vertex] == WHITE:
DFS_Visit(graph, adj_vertex)
elif self.visited[adj_vertex] == GREY:
self.circle += 1
self.visited[vertex] = BLACK
for vertex in range(numCourses):
if self.visited[vertex] == WHITE:
DFS_Visit(graph, vertex)
return self.circle == 0
- BFS:
In fact, BFS cannot be simply used as an edge detection paradigm, here’re some reasons:
Edge types are defined by DFS according to the text book
If u is BLACK and v is next to u, then (u, v) can either be BLACK or GREY
You can’t use distance as a flag because one might have different paths to same node
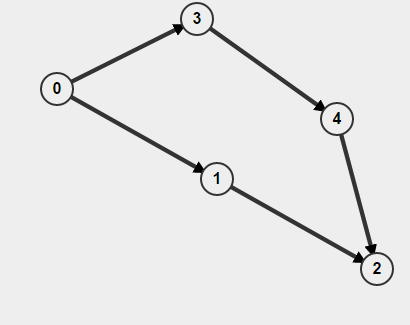
Topological Sort(BFS):
From `solution`__, BFS uses the indegrees of each node. We will first try to find a node with 0 indegree. If we fail to do so, there must be a cycle in the graph and we return false. Otherwise we have found one. We set its indegree to be -1 to prevent from visiting it again and reduce the indegrees of all its neighbors by 1. This process will be repeated for n (number of nodes) times. If we have not returned false, we will return true:
class Solution(object):
def canFinish(self, numCourses, prerequisites):
def buildGraph(graph, numCourses, edgelists):
for i in range(numCourses):
graph[i]
for edge in edgelists:
graph[edge[1]].append(edge[0])
return graph
def computeDegrees(graph, numCourses):
indegrees = [0]*numCourses
for values in graph.values():
for vertex in values:
indegrees[vertex]+=1
return indegrees
from collections import defaultdict
graph = defaultdict(list)
graph = buildGraph(graph, numCourses, prerequisites)
indegrees = computeDegrees(graph, numCourses)
queue = []
for i in range(numCourses):
if indegrees[i]==0:
queue.append(i)
# there's no vertex with 0 indegree which is a circle
if not queue:
return False
# you can check the degrees by calling each method, however, queue is most easy to understand following BFS pattern.
while queue:
vertex = queue.pop(0)
for adj_vertex in graph[vertex]:
indegrees[adj_vertex] -= 1
if indegrees[adj_vertex] == 0:
queue.append(adj_vertex)
return sum(indegrees) == 0
Topological Sort(DFS):
It’s safer to add one more step to calculate the indegrees, then we don’t need to worry about the order of input:
from collections import defaultdict
graph = defaultdict(list)
graph = buildGraph(graph, 5, [[0,5],[0,4],[2,5],[1,4],[3,2],[1,3]]) #[[1,0], [2,0], [3,1], [4,1], [2, 5]]
indegrees = indegrees(graph)
visited = [False] * len(graph.keys())
def dfs(graph, adj_vertex, visited, res):
visited[adj_vertex] = True
for vertex in graph[adj_vertex]:
if not visited[vertex]:
dfs(graph, vertex, visited, res)
res.append(adj_vertex)
res = []
for vertex in graph.keys():
if not visited[vertex]:
dfs(graph, vertex, visited, res)
print res[::-1]
Tarjan’s strongly connected components algorithm¶
https://en.wikipedia.org/wiki/Tarjan%27s_strongly_connected_components_algorithm
LeetCode 547. Friend Circles¶
From some source, we can visit every connected node to it with a simple DFS. As is the case with DFS’s, seen will keep track of nodes that have been visited.
For every node, we can visit every node connected to it with this DFS, and increment our answer as that represents one friend circle (connected component.)
solution:
class Solution(object):
def findCircleNum(self, M):
"""
:type M: List[List[int]]
:rtype: int
"""
visited = [False]*len(M)
count = 0
def dfs(M, visited, i):
for j in range(len(M)):
if M[i][j] == 1 and not visited[j]:
visited[j] = True
dfs(M, visited, j)
for i in range(len(M)):
if not visited[i]:
dfs(M, visited, i)
count+=1
return count
LeetCode 675. Cut Off Trees for Golf Event¶
The question is turned into finding distance between 2 trees. My original approach was to find the paths from (0, 0) to all trees which will be more complex because you don’t know how to handle the intermediate step.
- In order to implement the distance method, there’re 3 algorithms:
- BFS
- A* (Dijkstra’s special case)
- Hadlock
- Another trick is 2-direction BFS
Explaination is in sorce code:
class Solution(object):
def cutOffTree(self, forest):
"""
:type forest: List[List[int]]
:rtype: int
"""
# since the tree heights are ordered, we already have an order to cut these trees(have to cut the global min each time)
# then we can sort the tree node at the begining.
trees = []
for i in range(len(forest)):
for j in range(len(forest[0])):
if forest[i][j] > 1:
trees.append((forest[i][j], i, j))
trees = sorted(trees, key=lambda x: x[0])
def dist(forest, sr, sc, tr, tc):
# this array is to help go discover the grid
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
# we can't maintain a global visited helper map because previous search will
# change the trace
queue = [(sr, sc, 0)]
visited =[[False for _ in range(len(forest[0]))] for __ in range(len(forest))]
visited[sr][sc] = True
while queue:
r, c, d = queue.pop(0)
if r == tr and c == tc:
return d
for dx, dy in directions:
x = r + dx
y = c + dy
if 0 <= x < len(forest) and 0 <= y < len(forest[0]) and forest[x][y] and not visited[x][y]:
queue.append((x, y, d+1))
visited[x][y] = True
return -1
sr = sc = ans = 0
for _, tr, tc in trees:
d = dist(forest, sr, sc, tr, tc)
if d < 0:
return -1
ans += d
sr, sc = tr, tc
return ans
LeetCode 269. Alien Dictionary¶
When you are asked to get some kind of orders, think about Topological sort, but you first need to convert the question to a graph problem.